Mathematical functions for data science & artificial intelligence#
Algebraic functions#
Linear functions#
Tiene la forma de $\(f(x)=mx + b\)\( donde \)m\( y \)b\( \)\in R$.
\(m\) puede ser calculada por: $\(m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)$
y \(b\) es el punto de corte con el eje \(y\). Su dominio es \(Dom_{f} = (-\infty, \infty)\). Su imagen es \(Im_{f} = (-\infty, \infty)\)
coding a linear function#
import numpy as np
import matplotlib.pyplot as plt
N = 100
#slope
m = -1
#intercept
b = 3
#let's define the function
def f(x):
return (m*x + b)
#domain
x = np.linspace(-10,10, num=N)
#range
y = f(x)
fig, ax = plt.subplots()
ax.plot(x,y)
ax.grid()
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 2
1 import numpy as np
----> 2 import matplotlib.pyplot as plt
4 N = 100
6 #slope
ModuleNotFoundError: No module named 'matplotlib'
Polinomic functions#
Tiene la forma de $\(P(x)=a_{n}x^{n} + a_{n-1}x^{n-1}+...+a_{2}x^{2}+a_{1}x + a_{1}\)$
a una función que tiene esta forma se le llama polinomio de grado \(n\). A los elementos \(a\) los llamaremos coeficientes donde \(a \in R\).
Por ejemplo:
que es un polinomio de grado 7.
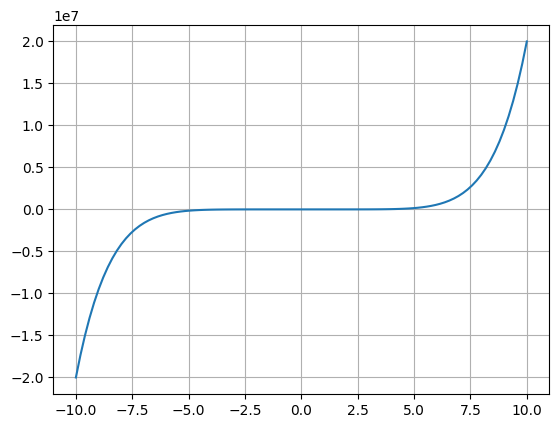
def f2(x):
return(2*(x**7) - x**4 + 3*(x**2) + 4)
y2 = f2(x)
fig, ax2 = plt.subplots()
ax2.plot(x,y2)
ax2.grid()
Power Function#
Hay unas funciones que son un caso particular de las funciones polinómicas que son las funciones potencia, las cuales tienen la forma:
Por ejemplo:
El dominio de \(f(x)=x^{2}\) es \(Dom_{f} = (-\infty, \infty)\). Su imagen es \(Im_{f} = [0, \infty)\)
Coding a power function#
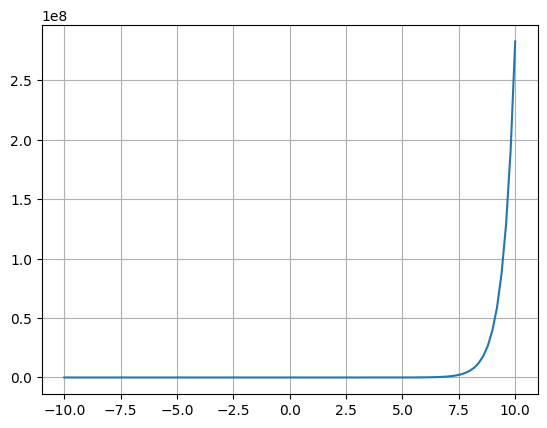
def f3(x):
return 7**x
y3 = f3(x)
fig, ax3 = plt.subplots()
ax3.plot(x,y3)
ax3.grid()
Trascendent functions#
these are functions that cannot be expressed as polynomials
Trigonometric functions#
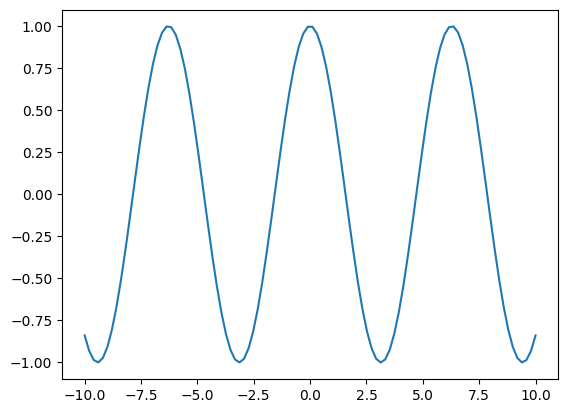
def f(x):
return np.cos(x)
y = f(x)
plt.plot(x,y)
[<matplotlib.lines.Line2D at 0x7f7f7b89f4c0>]
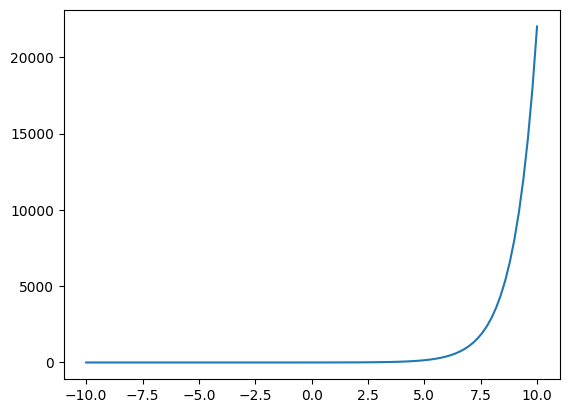
Exponential function#
Tienen la forma de $\(f(x)=a^x\)\( donde la base \)a$ es una constante positiva. Un gran ejemplo de una función exponencial es usando la base como el número de euler:
def f(x):
return np.exp(x) #euler
y=f(x)
plt.plot(x,y)
[<matplotlib.lines.Line2D at 0x7f7f7b82c4c0>]
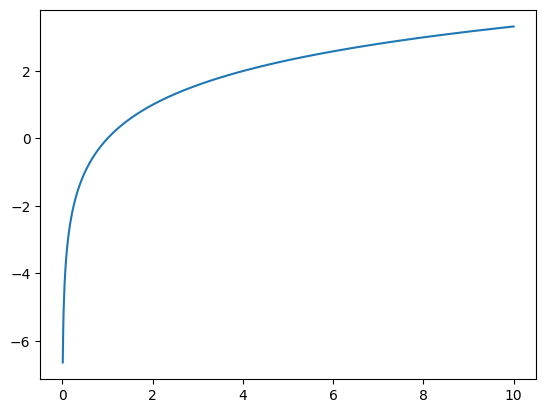
Logarithmic functions#
El logaritmo está definido por la relación:
donde:
\(b\) es la base.
\(n\) es el exponente al que está elevado la base.
\(x\) es el resultado de elevar la base \(b\) al exponente \(n\)
Ejemplo:
Teniendo b=2 y n=8, entonces:
Por lo que \(x=256\). Calculando el logaritmo base 2 de \(x\) es:
def f(x):
return np.log2(x)
#domain
x = np.linspace(0, 10, 1000)
plt.plot(x, f(x))
plt.show()
/tmp/ipykernel_224/3839064836.py:2: RuntimeWarning: divide by zero encountered in log2
return np.log2(x)
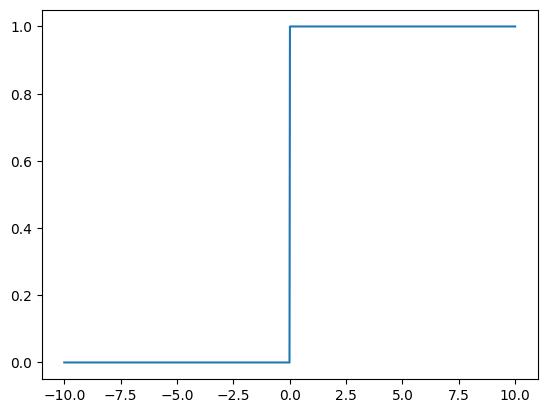
Heavyside function#
Son funciones que tienen diferentes valores definidos por un intervalo. Por ejemplo la función escalón de Heaviside:
x = np.linspace(-10, 10, 1000)
def f(x):
Y = np.zeros(len(x))
for index, x in enumerate(x):
if x >= 0:
Y[index] = 1
return Y
plt.plot(x, f(x))
plt.show
<function matplotlib.pyplot.show(close=None, block=None)>
x = np.linspace(-3, 3, 7)
#if you want to understand the enumerate:
type(enumerate(x))
for index, x in enumerate(x):
print("index is:", index)
print("value is:", x)
index is: 0
value is: -3.0
index is: 1
value is: -2.0
index is: 2
value is: -1.0
index is: 3
value is: 0.0
index is: 4
value is: 1.0
index is: 5
value is: 2.0
index is: 6
value is: 3.0
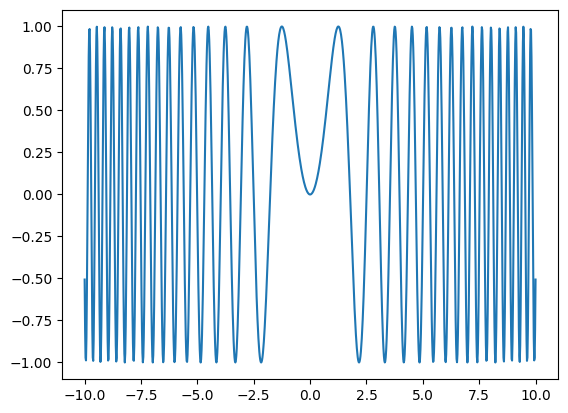
Composite functions#
import numpy as np
import matplotlib.pyplot as plt
N = 1000
x = np.linspace(-10,10, num=N)
def g(x):
return x**2
def f(x):
return np.sin(x)
y = g(x)
#this is basically plotting sin(x^2)
f_o_g = f(g(x))
plt.plot(x,f_o_g)
[<matplotlib.lines.Line2D at 0x7f7f7b7b30a0>]
How to manipulate functions#
Functions displacement#
Siendo \(c\) una constante mayor que cero, entonces la gráfica:
\(y=f(x)+c\) se desplaza \(c\) unidades hacia arriba.
\(y=f(x)-c\) se desplaza \(c\) unidades hacia abajo.
\(y=f(x-c)\) se desplaza \(c\) unidades hacia la derecha.
\(y=f(x+c)\) se desplaza \(c\) unidades hacia la izquierda.
N = 1000
def f(x):
return x**2;
c = 4
x = np.linspace(-10,10, num=N)
y = f(x + c) #note that this will displace y 4 units to the right
fig, ax = plt.subplots(nrows=1, ncols=2)
ax[0].plot(x, f(x)) #original cuadratic function
ax[0].grid()
ax[0].axhline(y=0, color='r')
ax[0].axvline(x=0, color='r')
ax[0].set_title("Original chart")
ax[1].plot(x,y) #function with transformation
ax[1].grid()
ax[1].axhline(y=0, color='r')
ax[1].axvline(x=0, color='r')
ax[1].set_title("Displaced chart")
Text(0.5, 1.0, 'Displaced chart')
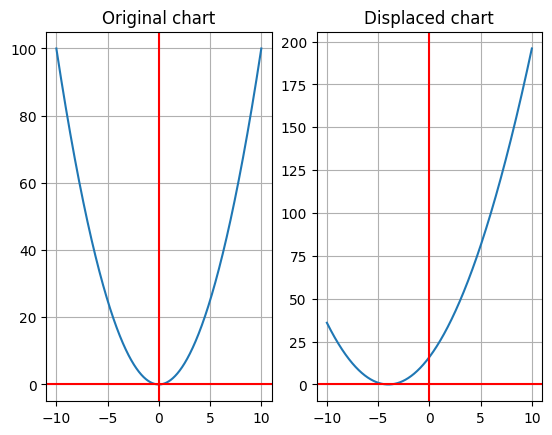
Functions elongations & compressions#
Siendo \(c\) una constante mayor que cero, entonces la gráfica:
\(y=c \cdot f(x)\) alarga la gráfica verticalmente en un factor de \(c\).
\(y= \frac{1}{c} \cdot f(x)\) comprime la gráfica verticalmente en un factor de \(c\).
\(y=f(c \cdot x)\) comprime la gráfica horizontelmente en un factor de \(c\).
\(y= f(\frac{1}{c} \cdot x )\) alarga la gráfica horizontelmente en un factor de \(c\).
N = 1000
def f(x):
return np.sin(x);
c = 2
x = np.linspace(-15,15, num=N)
y = f((1/c)*x) #note that this will elonge the chart in a proportion of 2
fig, ax = plt.subplots(nrows=1, ncols=2)
ax[0].plot(x, f(x)) #original sinusoidal function
ax[0].grid()
ax[0].axhline(y=0, color='r')
ax[0].axvline(x=0, color='r')
ax[0].set_title("Original chart")
ax[1].plot(x,y) #function with transformation (elonged horizontally)
ax[1].grid()
ax[1].axhline(y=0, color='r')
ax[1].axvline(x=0, color='r')
ax[1].set_title("Elonged chart")
Text(0.5, 1.0, 'Elonged chart')
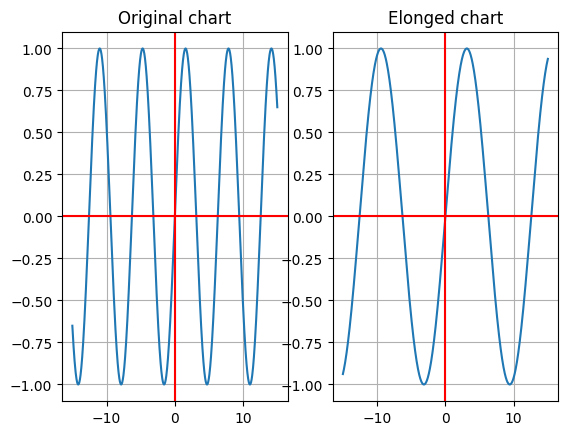
Function reflection#
\(y=-f(x)\) refleja la gráfica respecto al eje x.
\(y=f(-x)\) refleja la gráfica respecto al eje y.
N = 1000
def f(x):
return x**3;
x = np.linspace(-10,10, num=N)
y = f(-x) #this will reflect the function about the y axis
fig, ax = plt.subplots(nrows=1, ncols=2)
ax[0].plot(x, f(x)) #original cubic function
ax[0].grid()
ax[0].axhline(y=0, color='r')
ax[0].axvline(x=0, color='r')
ax[0].set_title("Original chart")
ax[1].plot(x,y) #function with transformation (reflected about the y axis)
ax[1].grid()
ax[1].axhline(y=0, color='r')
ax[1].axvline(x=0, color='r')
ax[1].set_title("Reflected chart")
Text(0.5, 1.0, 'Reflected chart')
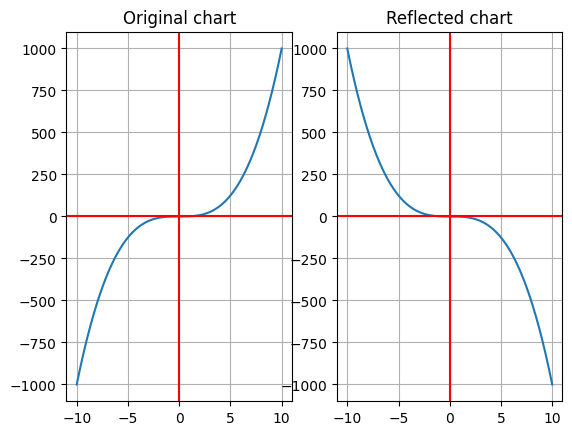
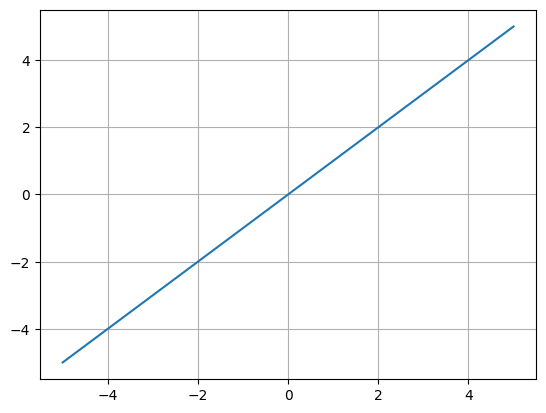
Activation Functions#
import numpy as np
import matplotlib.pyplot as plt
N = 1000
x = np.linspace(-5,5, num=N)
Linear function#
def f(x):
return x
plt.plot(x, f(x))
plt.grid()
heavyside function#
def H(x):
Y = np.zeros(len(x))
for idx,x in enumerate(x):
if x>=0:
Y[idx]=1
return Y
N=1000
y = H(x)
plt.plot(x,y)
plt.grid()
sigmoid function#
def f(x):
return 1/(1 + np.exp(-x))
N=1000
y = f(x)
plt.plot(x,y)
plt.grid()
hyperbolic tangent function#
def f(x):
return np.tanh(x)
N=1000
y = f(x)
plt.plot(x,y)
plt.grid()
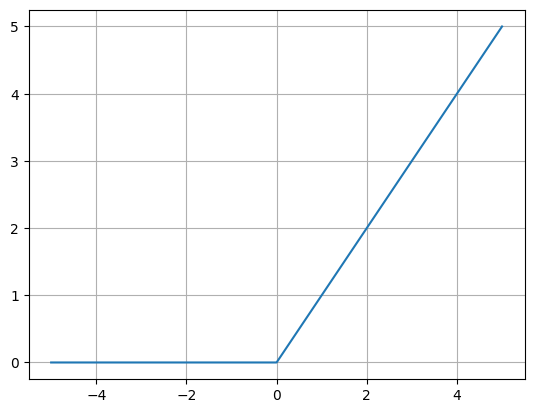
ReLu function#
def f(x):
return np.maximum(x,0)
N=1000
y = f(x)
plt.plot(x,y)
plt.grid()